In order to calculate the probability of P(Z<3), let's add all cases where Z<3:
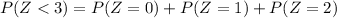
The minimum value of Z is given when X = 0 and Y = 1, so Z = 1.
The maximum value of Z is given when X = 1 and Y = 2, so Z = 3.
Therefore P(Z = 0) is zero.
Z = 1 can only happen when X = 0 and Y = 1.
Z = 2 can happen when X = 1 and Y = 1 or when X = 0 and Y = 2.
So we can rewrite the expression as follows:
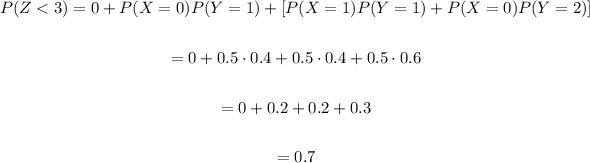
Therefore the correct option is A.