Question

A chef is going to use a mixture of two brands of italian dressing. the first brand contains 7% vinegar and the second brand contains 12% vinegar. the chef wants to make 280 milliliters of a dressing that is 9% vinegar. how much of each brand should she use

Answer 1

We know that

• The first brand contains 7% vinegar.

,

• The second brand contains 12% vinegar.

,

• The chef wants 280 milliliters with 9% vinegar.

Using the given information, we can express the following equation.

`0.07x+0.12(280-x)=0.09(280)`

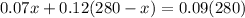
Notice that 0.07x represents the first brand, 0.12(280-x) represents the second brand, and 0.08(280) represents the final product the chef wants to make.

Let's solve for x.

`\begin{gathered} 0.07x+33.6-0.12x=25.2 \\ -0.05x=25.2-33.6 \\ -0.05x=-8.4 \\ x=(-8.4)/(-0.05) \\ x=168 \end{gathered}`

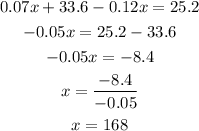
Therefore, the chef needs 168 of the first brand and 112 of the second brand.

Notice that 280-168 = 112.