By definition, a perfect square trinomial is a trinomial that can be written as the square of a binomial. It is in the form:
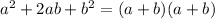
The simple trinomial is in the form:

Not all the simple trinomials can be written as the square of a binomial, then we need to check if the trinomial follows the structure of the perfect square trinomial. If it doesn't, then the factors won't be the same, and this is the main difference.
a. The given trinomial is:

If it is a perfect square trinomial then:
![\begin{gathered} a^2=x^2 \\ a=x \\ b^2=6 \\ b=\sqrt[]{6} \\ 2ab=5x \\ 2\cdot x\cdot\sqrt[]{6}\\e5x \\ \text{Then it is not a perfect square trinomial} \\ x^2+5x+6=(x+3)(x+2)\text{ It is a simple trinomial} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c0ktqb8mozvjdqcuf8tbtgy5x7kr7xcvdp.png)
b. The given trinomial is:
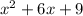
Let's check if it is a perfect square trinomial:
![\begin{gathered} a^2=x^2\to a=x \\ b^2=9\to b=\sqrt[]{9}=3 \\ 2ab=2\cdot x\cdot3=6x \\ \text{This is a perfect square trinomial, then } \\ x^2+6x+9=(x+3)(x+3)=(x+3)^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3a8q6i0dtalfcxsb7940bow56c9ops8h3w.png)