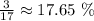Question

Find the probability that a randomly chosen point is the figure lies in the shaded region. Give all answers in fraction and percent forms.help with number 5 or all of them if u can pls

Answer 1

NUMBER 5:

INFORMATION:

We have a trapeze and, we need to find the probability that a randomly chosen point is the figure lies in the shaded region

STEP BY STEP EXPLANATION:

To find the probability, we must divide the area of the shaded region by the total area of the trapeze

`\text{ Probability}=\frac{Shaded\text{ area}}{Total\text{ area}}`

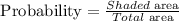
- Total area:

To calculate the total area, we must use the formula for the area of a trapeze

`A_(trapeze)=((b_1+b_2)h)/(2)`

Where, b1 and b2 are the bases and h is the height

Then, analyzing the trapeze we can see that b1 = 20, b2 = 14 and h = 12

`A_(total)=A_(trapeze)=((20+14)12)/(2)=204`

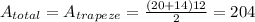
So, the total area is 204 square units

- Shaded area:

To find the shaded area, we must subtract the no shaded area from the total area.

We can see that the no shaded area is a rectangle with width = 14 and height = 12

Now, using the formula for the area of a rectangle

`A_(rectangle)=\text{ width}*\text{ height}=14*12=168`

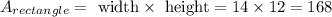
Then, subtracting the area of the rectangle from the total area

`A_{\text{ no shaded}}=204-168=36`

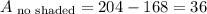
So, the no shaded are is 36 square units.

Finally, the probability would be

`\begin{gathered} \text{ Probability}=(36)/(204) \\ \text{ Simplifying,} \\ (3)/(17)\approx17.65\text{ \%} \end{gathered}`

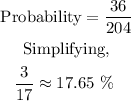
ANSWER:

the probability that a randomly chosen point is the figure lies in the shaded region is

`(3)/(17)\approx17.65\text{ \%}`