Question

in the lab Dale has two solutions that contain alcohol and is mixing them each other.she uses four times as much solution A as solution B.solution a is 20% of alcohol and solution B is 15% of alcohol. how many milliliters of solution B does he use, if the was resulting mixtures has 570 milliliter of pure alchohol.number of milliliters of solution B__?

Answer 1

Let:

• A ,be the number of millilitres (mL) of solution A used.

,

• B ,be the number of mL of solution B used.

We know that Dale uses four times as much solution A as solution B, meaning

`A=4B`

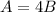
Now, we know that we will end up with 570 mL of pure alcohol in the final solution. Using the dilution of both A and B (20% means 0.2 and 15% is 0.15) we would have that:

`0.2A+0.15B=570`

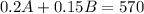
We would have the following system of equations:

`\begin{cases}A=4B \\ 0.2A+0.15B=570\end{cases}`

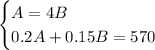
Substituting equation 1 in equation 2 and solving for B :

`\begin{gathered} 0.2A+0.15B=570 \\ \rightarrow0.2(4B)+0.15B=570 \\ \rightarrow0.8B+0.15B=570 \\ \rightarrow0.95B=570\rightarrow B=(570)/(0.95) \\ \Rightarrow B=600 \end{gathered}`

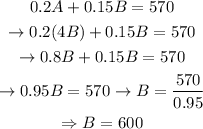
Substituting in equation 1 and solving for A:

`\begin{gathered} A=4B \\ \rightarrow A=4(600) \\ \Rightarrow A=2400 \end{gathered}`

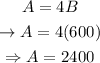
This way, we can conclude that 2400 mL of solution A and 600mL of solution B were used.