Question

Please help me with my calc hw, I'd be more than happy to chip in albeit with my limited knowledge.

Answer 1

Given:

`F(x)=\int_0^x√(36-t^2)dt`

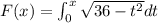
Required:

To find the range of the given function.

Step-by-step explanation:

The graph of the function

`y=√(36-t^2)`

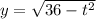
is upper semicircle with center (0,0) and radius 6, with

`-6\leq t\leq6`

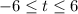
So,

`\int_0^x√(36-t^2)dt`

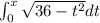
is the area of the portion of the right half of the semicircle that lies between

t=0 and t=x.

When x=0, the value of the integral is also 0.

When x=6, the value of the integral is the area of the quarter circle, which is

`(36\pi)/(4)=9\pi`

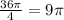
Therefore, the range is

`[0,9\pi]`

Final Answer:

The range of the function is,

`[0,9\pi]`