Solution:
Given that;
y varies directly with the square of x
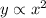
This expression above becomes
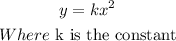
When
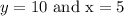
Substitute the values for x and y into the expression above to find k
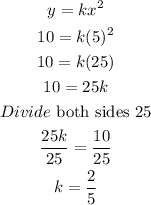
The expression becomes
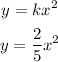
a) The value of y when x = 20
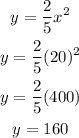
Hence, the value of y is 160
b) The value of x when y = 40
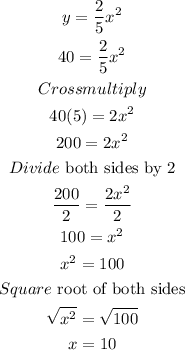
Hence, the value of x is 10