Question

See attached pic for problem. Only need help with #2

Answer 1

Part 1

The independent variable are the predicting varaible for which other variable are depends on. The are the x- values

Hence

The indepedent varibles is school year

The dependent variable are the responses variables. They are the y-values for which depends on othere values,

Hence

The dependent variable for the data given is

The Tution

Part 2

To find the function, we need to set up the data as given in the table below.

The years has an interval of 1 and each fees difer by 4, the to obtain the x-values we use the mid-point

`x=\frac{\text{lower}+\text{higher}}{2}\text{ for each }`

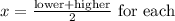
Hence

The data plot will be

The linear is given by the form

`\begin{gathered} y=ax+b \\ \text{Where }^{} \\ a=561.043,\text{ b=-0.0000}010994 \\ \text{Hence } \\ y=561.043x-0.0000010994 \end{gathered}`

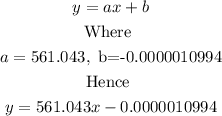
THerefore

The linear regression is y = 561. 043x -0.0000010994

Then for exponenetial we have

`\begin{gathered} y=e^(ax+b) \\ \text{Where } \\ a=0.0286229,b=-47.2727 \\ \text{Hence } \\ y=e^(0.029x-47.27) \end{gathered}`

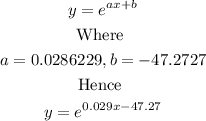
Hence

The exponential regression is y = e^(0.029x-47.27)

For the power represion we have

`\begin{gathered} y=ab^x \\ \text{Where } \\ a=2.9495*10^(-21,)b=1.02904 \\ \text{Hence } \\ y=2.9495*10^(-21,)(1.02904)^x \end{gathered}`

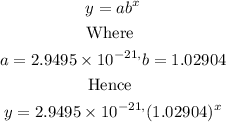
Hence

The power regression is

y= 2.9495 x 10^-21 (1.02904)ˣ

Part 3

The graoh lot for linear function is given below

The graph for the exponential plot is

The graph for the power regression plot is given below as