Question

Write an equation of a circle with diameter AB.A(1,1), B(11,11)Choose the correct answer below.A. (X-6)2 + (y-6)2 = 11C. (x-6)2 – (y+6)2 = 50E. (X+6)2 + (y-6)2 = 50G. (X+6)2 – (y + 6)2 = 50

Answer 1

The question asks us to find the equation of a circle with diameter AB with coordinates:

A = (1, 1), B = (11, 11)

In order to solve this, we need to know the general form of the equation of a circle.

The general form of the equation of a circle is given by:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ \text{where,} \\ (a,b)=\text{ coordinates of the center of the circle} \\ r=\text{radius of the circle} \end{gathered}`

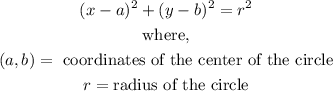
We have been given the coordinates of the diameter. This means that finding the midpoint of the diameter

will give us the center coordinates of the circle, which is (a, b).

The formula for finding the midpoint of a line is given below:

`\begin{gathered} (x,y)=(x_2+x_1)/(2),(y_2+y_1)/(2) \\ \text{where,} \\ x_2,y_2=\text{ second coordinate} \\ x_1,y_1=\text{first coordinate} \end{gathered}`

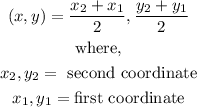
For better understanding, a sketch is made below:

Therefore, let us find the coordinates of the center of the circle using the midpoint formula given above:

`\begin{gathered} a,b=(x_2+x_1)/(2),(y_2+y_1)/(2) \\ x_2=11,y_2=11 \\ x_1=1,y_1=1 \\ \\ \therefore(a,b)=(11+1)/(2),(11+1)/(2) \\ \\ (a,b)=6,6 \\ Thus, \\ a=6,b=6 \end{gathered}`

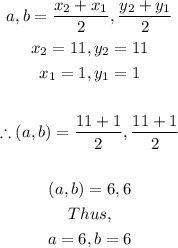
Now that we have the coordinates of the center, we now need to find the value of the radius of the circle.

This is done by finding the length from the center of the circle to any side of the diameter.

Let us use from point (6,6) which is the center to the point (11, 11) which is one side of the diameter.

The formula for finding the distance between two points is given by:

`\begin{gathered} |\text{distance}|^2=(y_2-y^{}_1)^2+(x_2-x_1)^2_{} \\ \text{where,} \\ x_2,y_2=\text{second point} \\ x_1,y_1=\text{first point} \end{gathered}`

hence, we can now find the square of the radius as:

`\begin{gathered} r^2=(y_2-y^{}_1)^2+(x_2-x_1)^2_{} \\ x_2,y_2=11,11_{} \\ x_1,y_1=6,6 \\ \\ \therefore r^2=(11-6)^2+(11-6)^2 \\ r^2=5^2+5^2 \\ r^2=25+25 \\ \therefore r^2=50 \end{gathered}`

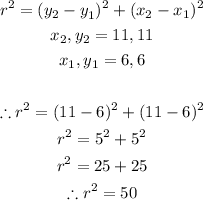
Now that we have the radius, we can now compute the equation of the circle as:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ a=6,b=6,r^2=50 \\ \\ \therefore(x-6)^2+(y-6)^2=50\text{ (Option B)} \end{gathered}`

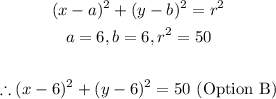
A graph of the circle is given below: