Question

I was doing this with a tutor but there was a connection problem.

Answer 1

`(x-3)^2+(y+7)^2=113`

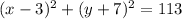
The point (7,6) is not on the circle

Explanation:

(a)

The equation of the circle is given as follows:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \text{ where (h,k) is the center and r is the radius } \end{gathered}`

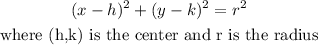
We replace to calculate the radius of the circle, like this:

`\begin{gathered} \mleft(-4-3\mright)^2+\mleft(1-\mleft(-7\mright)\mright)^2=r^2 \\ (-7)^2+(8)^2=r^2 \\ r^2=113 \end{gathered}`

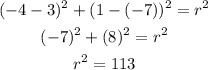
Therefore, the equation would be:

`(x-3)^2+(y+7)^2=113`

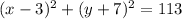
(b)

We replace the point, and if the value is greater than the radius, it means that this point is not on the circle:

`\begin{gathered} (x-3)^2+(y+7)^2\le113 \\ \text{ replacing:} \\ \mleft(7-3\mright)^2+\mleft(6+7\mright)^2\le113 \\ 4^2+13^2\le113 \\ 16+169\le113 \\ 185\le113 \end{gathered}`

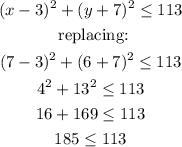
Therefore, the point (7,6) is not on the circle