Question

Liz is collecting aluminum cans for a school fundraiser. So far, she has collected 16 cans, which is 20% of her goal. How many cans must she collect to reach her goal?Parts A & B

Answer 1

Given the word problem, we can deduce the following information:

1. Liz collected 16 cans, which is 20% of her goal.

To determine the number of cans that Liz needs to collect to reach her goal, we use below equation:

`0.20x=16`

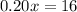
where:

x= total number of cans that Liz needs to collect

So,

`\begin{gathered} 0.20x=16 \\ \text{Simplify} \\ x=(16)/(0.20) \\ x=80 \end{gathered}`

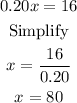
Hence, the total number of cans is 80.

A.

To complete the double number line, we must determine first the other percent values. It the goal is 100%, we must subtract 20% from 100% and divide it by 4 to get the remaining percent values. So,

`(100-20)/(4)=20`

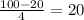
So the other percent values are:

0%

20%

20%+20%=40%

40%+20%=60%

60%+20%=80%

80%+20%=100%

To determine the amount of cans for each percent value,the process is shown below:

`80((40)/(100))=32`
`\begin{gathered} 80(.6)=48 \\ \end{gathered}`
`80(.8)=64`
`80((100)/(100))=80`

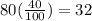
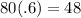
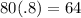
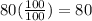
Therefore, the answer for double number line is:

Cans : 0 16 32 48 64 80

Percent : 0% 20% 40% 60% 80% 100%

B.

Based on the information gathered from A, for every 16 cans Liz collects, she adds 20% toward her goal. She will have 32 cans if she reaches 40% of her goal. Liz must collect 80 cans to reach her goal.