The equation of a line given in slope-intercept form is written as
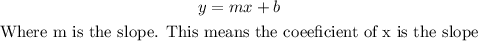
For two lines to be parallel, their slopes must equal to each other. Also for the two lines to be perpendicular, their slopes must be a negative inverse of each other. An example of negative inverse is given as;

The slope of the first line is 1, since the line is given as,
y = x - 8
(The coefficient of x is 1)
The slope of the second line is -1, since the line is given as,
y = -x + 8
(The coefficient of x is -1)
Therefore, since both slopes are not equal and not negative inverses of each other, then the correct answer is NEITHER.