Question

A bag contains 4 blue and 6 white tokens. Two tokens are drawn from the bag one after another, without replacement. Find the probability that: the first is blue and the second is white.

Answer 1

Concept; Probability

Step1: The total number of tokens is

`6\text{white +4 Blue}=\text{ 10 tokens}`

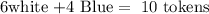
let the probability of blue be P(B) and the probability of red be P(R)

The probability that the first is Blue is

`\begin{gathered} P(B)=\frac{number\text{ of blue }}{total\text{ number of tokens}}=(4)/(10)=(2)/(5) \\ \end{gathered}`

The probability the second is white without replacement is

`P(R)=\frac{number\text{ of white}}{total\text{ token}}=(6)/(9)=(2)/(3)`

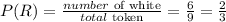
Hence the combined probability of Blue and Red is

`P(BR)=(2)/(5)*(2)/(3)=(4)/(15)`

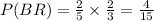
Therefore the probability that the first is blue and the second is white is 4/15