Step-by-step explanation
Step 1
Let
a) for ball 1

the formula for the distance is given by:
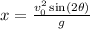
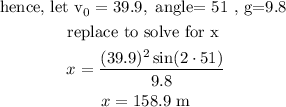
hence, the horizontal distance reached by the ball 1 is 158.9 meters
Step 2
as the ball started from the same point at the same initial speed, the only way to make the second ball hits the same point as the first is thworing the second ball at the same angle, it is 51 °