Question

Question 39.Find the inverse of the given function. Graph both functions on the some set of axes and show the line y=x as a dotted line in the graph.

Answer 1

First, to find the inverse of a function, call the original function "x" and call call "x" in the original function as the inverse function:

`\begin{gathered} f(x)=5x+1 \\ x=5f^(-1)(x)+1 \end{gathered}`

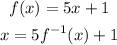
Now, we solve for the inverse function:

`\begin{gathered} x=5f^(-1)(x)+1 \\ 5f^(-1)(x)+1=x \\ 5f^(-1)(x)=x-1 \\ f^(-1)(x)=(x)/(5)-(1)/(5) \end{gathered}`

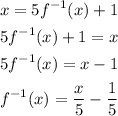
To graph lines, we can find two points in it and draw a line that passes through both.

Let's pick x = 0 and x = 1 for the first equation:

`\begin{gathered} f(0)=5\cdot0+1=1 \\ f(1)=5\cdot1+1=6 \end{gathered}`

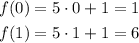
So, we plot the points (0, 1) and (1, 6).

For the inverse, we can simply invet the coordinates, which is the same as picking x = 1 and x = 6:

`\begin{gathered} f^(-1)(1)=(1)/(5)-(1)/(5)=0 \\ f^(-1)(6)=(6)/(5)-(1)/(5)=(5)/(5)=1 \end{gathered}`

Thus, we have the points (1, 0) and (6, 1).

The line y = x is jus the diagonal that passes though point (0, 0) and (1, 1), for example.

Putting these points and drawing the lines, we get: