Question

A chemical company makes two brand of antifreeze. The first brand is 70 % pure antifreeze, and the second brand is 95% pure antifreeze. In order to obtain 110 gallons of a mixture that contains 85% pure antifreeze, how many gallons of each brand of antifreeze must be used?first brand:_____gallonssecond brand:_____gallons

Answer 1

Since the 1st brand is 70% pure antifreeze

Since the 2nd brand is 95% pure antifreeze

Since we need to obtain 110 g of a mixture that contains 85% pure antifreeze

Let the quantity of the first is x and the second is y

Then

`(70)/(100)x+(95)/(100)y=(85)/(100)(110)`
`0.7x+0.95y=93.5\text{ (1)}`
`x+y=110\text{ (2)}`

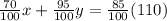
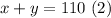
Now let us solve the two equations to find x and y

Multiply equation (2) by -0.7

`\begin{gathered} (-0.7)x+(-0.7)y=(-0.7)110 \\ -0.7x-0.7y=-77\text{ (3)} \end{gathered}`

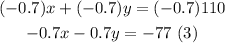
Add equations (1) and (3)

`\begin{gathered} (0.7x-0.7x)+(0.95y-0.7y)=(93.5-77) \\ 0+0.25y=16.5 \\ 0.25y=16.5 \end{gathered}`

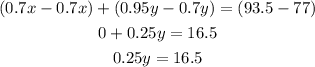
Divide both sides by 0.25

`\begin{gathered} (0.25y)/(0.25)=(16.25)/(0.25) \\ y=66 \end{gathered}`

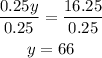
Substitute the value of y in equation (2) to find x

`x+66=110`

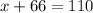
Subtract 66 from both sides

`\begin{gathered} x+66-66=110-66 \\ x+0=44 \\ x=44 \end{gathered}`

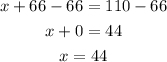
First brand: 44 gallons

Second brand: 66 gallons