Question

1. P(video games and kid is 10 to 12 years old)2. P(basketball/kid is 13 to 15 years old)3. P(kid is 13 to 15 years old/basketball)4. P(darts/kid is 10 to 15 years old)5. P(basketball and darts)6. P(basketball and kid is 13 to 18 years old)Answer the following problems about two way frequency tables make sure to reduce your fraction.

Answer 1

1. P(video games and kid is 10 to 12 years old)

`\begin{gathered} P(video\text{ games and kid i 10 to 12 years old)} \\ =\text{ }\frac{number\text{ of kids 10 - 12 years old playing video games}}{total\text{ number of students}} \\ =\text{ }(17)/(143) \end{gathered}`

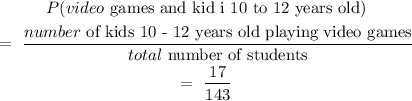
Therefore,

The P(video games and kid is 10 to 12 years old) = 17/143

2. P(basketball/kid is 13 to 15 years old)

`\begin{gathered} P\mleft(basketball/kid\text{ is 13 to 15 years old}\mright)\text{ } \\ =\text{ }\frac{number\text{ of kids 13 - 15 years old playing basketball}}{number\text{ of kids of age 13 to 15 years old}} \\ =\text{ }(14)/(45) \end{gathered}`

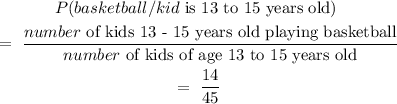
P(basketball/kid is 13 to 15 years old) = 14/45

3. P(kid is 13 to 15 years old/basketball)

`\begin{gathered} P(\text{kid is 13 to 15 years old / basket ball)} \\ =\text{ }\frac{number\text{ of kids aged 13 to 15 years old }}{number\text{ of kids playing basketball}} \\ =\text{ }(14)/(54) \\ =\text{ }(7)/(27) \end{gathered}`

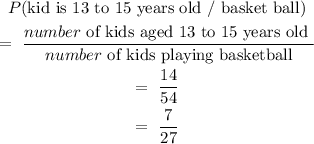
P(kid is 13 to 15 years old/basketball) = 7/27

4. P(darts/kid is 10 to 15 years old)

`\begin{gathered} P(\text{darts / kid is 10 to 15 years old)} \\ =\text{ }\frac{number\text{ of kids age 10 to 15 playing darts}}{\text{number of kids age 10 to 15}} \\ =\text{ }\frac{kids\text{ age 10 to 12 + age 13 to 15 playing darts}}{\text{kids age 10 to 12 + age 13 to 15}} \\ =\text{ }\frac{12\text{ + 15}}{34\text{ + 45}} \\ =\text{ }(27)/(79) \end{gathered}`

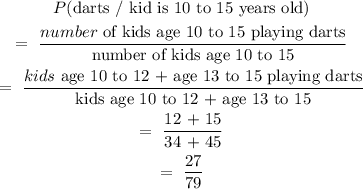
P(darts/kid is 10 to 15 years old) = 27/79

5. P(basketball and darts)

`\begin{gathered} P(basketball\text{ and darts)} \\ \sin ce\text{ there are no kids playing basketball and darts at the } \\ \text{same time} \\ \text{then,} \\ P(basketball\text{ and darts) = 0} \end{gathered}`

P(basketball and darts) = 0

6. P(basketball and kid is 13 to 18 years old)

`\begin{gathered} P(\text{basketball and kid is 13 to 18 years old)} \\ =\text{ }\frac{number\text{ of kids 13 to 18 years playing basket}}{nu\text{mber of kid 13 to 18 years }} \\ =\text{ }\frac{\text{kids 13 to 15 years + 16 - 18 years playing basketball}}{\text{kids 13 to 15years + 16 to 18 years}} \\ =\text{ }\frac{14\text{ + 18}}{45\text{ + 35}} \\ =\text{ }(32)/(80) \\ =(2)/(5) \end{gathered}`

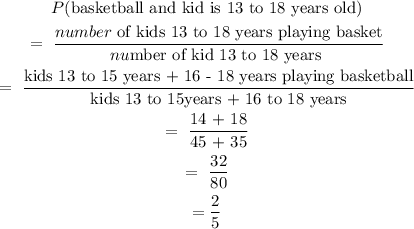
P(basketball and kid is 13 to 18 years old) = 2/5