To solve the exercise, it is helpful first to draw the situation that the statement describes:
The total area of the figure will be
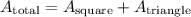
Then, we can calculate the area of the square using the following formula:
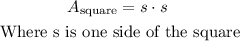
So, we have:

Now, we can calculate the area of the triangle using the following formula:

So, we have:
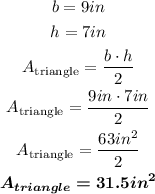
Finally, we calculate the total area of the figure
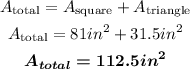
Therefore, the total area of the figure is 112.5 square inches, and the correct answer is option C.