ANSWER
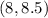
Step-by-step explanation
When a line segment is divided by ratio m:n, the coordinates of the point of division are given as:
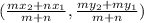
where (x₁, y₁) and (x₂, y₂) are the coordinates of the ends of the line.
Therefore, we have that:
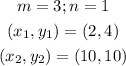
Therefore, the coordinates of point C are:
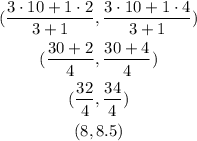
Those are the coordinates of C.