We are given that the height of a rock in terms of the time is given by the following equation:

We are asked to determine the height after two seconds. To do that we will substitute in the equation the value of "t = 2s", like this:
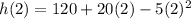
Solving the operations we get:
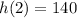
Therefore, the height after 2 seconds is 140 ft.
Now, to determine an equation for the velocity we will determine the derivative with respect to the time of the equation for the height.
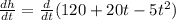
Now, we distribute the derivative:
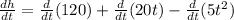
For the first derivative we will use the following rule:
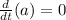
Where "a" is a constant. Applying the rule we get:
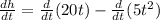
For the second derivative we will use the following rule:

Where "a" is a constant. Applying the rule we get:
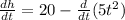
For the last derivative we will use the following rule:
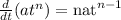
Applying the rule we get:
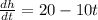
Since the derivative of the position with respect to time is the velocity we have:
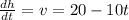
Now, we substitute the value of "t = 2s":
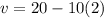
Now, we solve the operations:
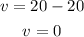
Therefore, the velocity after 2 seconds is 0.