Question

A recent math test had an average score of 75, with a standard deviation of 10. What percentage of people scored an 85 or higher?16%34%50%, 13.5%

Answer 1

16%.

Explanation:

In a recent math test:

• The average score = 75

,

• Standard Deviation = 10

To find: The percentage of people who scored an 85 or higher, P(X>85).

First, find the z-score when X=85.

`z-score=(X-\mu)/(\sigma)`

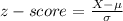
Substitute the given values:

`z=(85-75)/(10)=(10)/(10)=1`

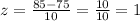
The people who scored an 85 or higher are 1 standard deviation away from the mean.

`13.5\%+2.35\%+0.15\%=16\%`

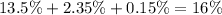
The percentage of people who scored an 85 or higher is 16%.