Answer:
• Mean Slope = -7
,
• c=0.5
Explanation:
Given the function:
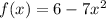
Part A
We want to find the mean slope on the interval [-6, 7].
First, evaluate f(7) and f(-6):
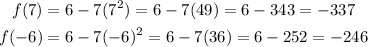
Next, substitute these values into the formula for the mean slope.
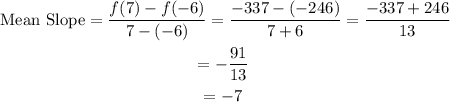
The mean slope of the function over the interval [-6,7] is -7.
Part B
Given the function, f(x):
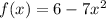
Its derivative, f'(x) will be:
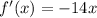
Replace c for x:
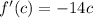
Equate f'(c) to the mean slope obtained in part a.
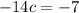
Solve for c:
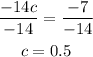
The value of c that satisfies the mean value theorem is 0.5.