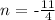A) We need to find the rate of change of the function first.
The rate of change or slope of the line is:
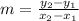
Where x and y are the coordinates of a point in line.
In order to calculate the slope we can take the poinst:
x1 = -6, y1 = 4
x2 = -2, y2= 1
Using the formula of above we find that the slope is:
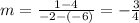
Now, in order to find the value of y-intercept of the line we can use formula:
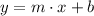
Which is the function of the line. From the formula of above we don't know the value of b (the y-intercept).
But we know that the formula must be valid for a point in the line. We can find the value of b replacing the coordinates of a point in the line, let's choose: x = -6 and y = 4, so:
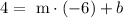
Now we use the value of m of above:
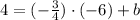
And from the last equation we can see that:
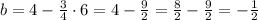
So, the equation of the line is:
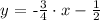
And the y-intercept is obtain replacing x = 0, so the y-intercept is: y = -1/2
b) From the stepts of above we already know an equation that represents the function! It is:
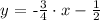
c) Now, we need to use the last equation to find y = n in the table. We know from the table that the value x for that value of y is x = 3, so we replace that value in the equation of the line:
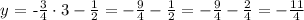
So the value of n is: