Question

Find the value of X and y if l || m.

Answer 1

The Solution.

Step 1:

We shall find two equations from the given angles.

First, by vertically opposite angle property of angles between two lines, we have that:

`\begin{gathered} 7y-23=23x-16 \\ \text{Collecting the like terms , we get} \\ 7y-23x=23-16 \\ 7y-23x=7\ldots.eqn(1) \end{gathered}`

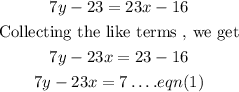
Similarly, by alternate property of angles between lines, we have that:

`\begin{gathered} 23x-16+8x-21=180 \\ \text{Collecting like terms, we get} \\ 31x-37=180 \\ 31x=180+37 \\ 31x=217 \\ \text{Dividing both sides by 31, we get} \\ x=(217)/(31)=7 \end{gathered}`

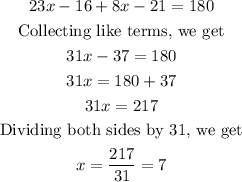
Step 2:

We shall find the values of y by substituting 7 for x in eqn(1), we get

`\begin{gathered} 7y-23(7)=7 \\ 7y-161=7 \\ 7y=7+161 \\ 7y=168 \\ \text{Collecting the like terms, we get} \\ y=(168)/(7)=24 \end{gathered}`

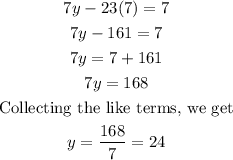
Step 3:

Presentation of the Answer.

The correct answers are; x = 7 , and y = 24