Answer:
The length of the side of the square is approximately
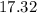 feet, which lies between the whole numbers
feet, which lies between the whole numbers
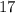 and
and
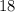 .
.
Explanation:
Step 1: Assume your variable
Since all the sides of a square are the same, let's consider the side to be the variable:
 .
.
Step 2: Create an equation
The formula for the area of a square is:
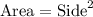
We have assumed the side to be
 , and the area is said to be
, and the area is said to be
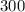 , so substitute these values into the formula:
, so substitute these values into the formula:

Step 3: Solve the equation
Using the formula for the area of a square, we came to find an equation:
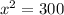
Now, let's find the value of
 :
:

The length of the side of the square is approximately
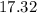 feet.
feet.
As we know, this number lies between
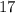 and
and
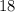 .
.