ANSWER
40807 cm³/min
Step-by-step explanation
The tank has the shape of a cone, with a total height of 9 meters and a diameter of 3.5 m - so the radius, which is half the diameter, is 1.75 m. As we can see, the relationship between the height of the cone and the radius is,

So the volume of water will be given by,

Where h is the height of the water (not the tank).
If we derive this equation, we will find the rate at which the volume of water is changing with time,
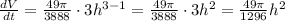
We want to know what is the change of volume with respect to time, and this is,
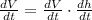
Because the height also changes with time. We know that this change is 24 cm per minute when the height of the water in the tank is 1 meter (or 100 cm), so we have,

This is the rate at which the water is increasing in the tank. However, we know that there is a leak at a rate of 12300 cm³/min, which means that in fact the water is being pumped into the tank at a rate of,
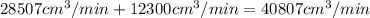
Hence, the water is being pumped into the tank at a rate of 40807 cm³/min, rounded to the nearest whole cm³/min.