To find the area of the window you need to find the area of rectangular part and the area of semicircle part.
To find the area of the rectangular part you need to find the height of the rectangle, use the perimeter to find it:
Perimeter of the given window is equal to: The circunference or perimeter of the semicircle (πr) and the perimeter of the rectangular part (w+2h)
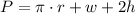
The radius of the semicircle is equal to the half of the width:
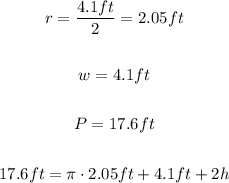
Use the equation above and find the value of h:
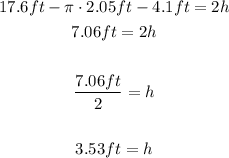
Find the area of the rectangular part:
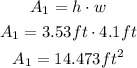
Find the area of the semicircle:
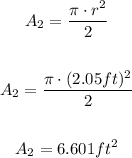
Sum the areas to get the area of the window:
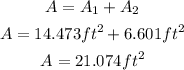
Then the area of the window is 21.07 squared feet