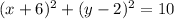Question

Find a standard form of the equation for the circle with the following property

Answer 1

Given:

`Endpoints\text{ }(-7,5)\text{ and }(-5,-1)`

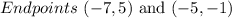
To get the equation of the circle, the center of the circle and the radius are needed.

The center of the circle is the midpoint of the endpoints.

Using the midpoint formula;

`\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ where: \\ x_1=-7,y_1=5 \\ x_2=-5,y_2=-1 \end{gathered}`

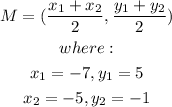
Thus,

`\begin{gathered} M=((-7+(-5))/(2),(5+(-1))/(2)) \\ M=((-12)/(2),(4)/(2)) \\ M=(-6,2) \end{gathered}`

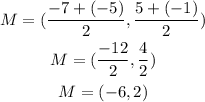
Hence, the coordinates of the center of the circle is (-6,2)

The length of the diameter can be gotten using the distance between two points formula;

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`\begin{gathered} where: \\ x_1=-7,y_1=5 \\ x_2=-5,y_2=-1 \\ Hence, \\ d=√((-5-(-7))^2+(-1-5)^2) \\ d=√(2^2+(-6)^2) \\ d=√(4+36) \\ d=√(40) \end{gathered}`

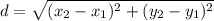
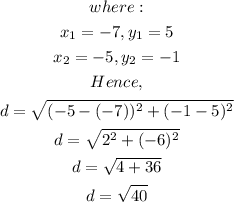
The diameter is twice the radius. Hence, the radius is;

`\begin{gathered} r=(d)/(2) \\ r=(√(40))/(2)=(2√(10))/(2) \\ r=√(10) \end{gathered}`

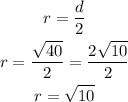
Hence, the equation of the circle with center (-6,2)

`with\text{ radius }√(10)`

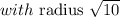
Using the standard form of the equation of a circle;

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ where: \\ (h,k)\text{ }is\text{ }the\text{ center} \\ r\text{ is the radius} \\ h=-6 \\ k=2 \\ r=√(10) \end{gathered}`

Hence, the equation is;

`\begin{gathered} (x-(-6))^2+(y-2)^2=(√(10))^2 \\ (x+6)^2+(y-2)^2=10 \end{gathered}`

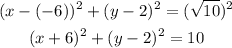
Therefore, the equation of the circle is;

`(x+6)^(2)+(y-2)^(2)=10`