Question

Part of a light ray striking an interface between air and water is refracted, and part is reflected, as shown. The index of refraction of air is 1.00 and the index of refraction of water is 1.33. The frequency of the light ray is 7.85 x 10^16 Hz.(a) If angle 1 measures 40°, find the value of angle 2.(b) If angle 1 measures 40°, find the value of angle 3.(c) Calculate the speed of the light ray in the water.(d) Calculate the wavelength of the light ray in the water.(e) What is the largest value of angle 1, that will result in a refracted ray?

Answer 1

We will use Snell's law, which states:

`n_1\sin \theta_1=n_2\sin \theta_2`

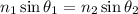
Where n1 and n2 are the refraction indexes and their respective angles are "theta1" and "theta2".

For part A we replace the values:

`1\sin 40=1.33\sin \theta_2`

Now we solve for "theta2" first by dividing both sides by 1.33:

`(\sin40)/(1.33)=\sin \theta_2`

Now we use the inverse function for sine:

`\arcsin ((\sin 40)/(1.33))=\theta_2`

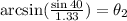
Solving the operation:

`28.9=\theta_2`

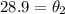
For part B, since "theta1" and "theta3" are angles of reflection, according to the reflection law, these angles are equal, therefore:

`\theta_3=\theta_1=40`

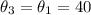
For part C. The index of refraction is defined as:

`n=(c)/(v)`

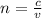
Where "c" is the speed of light in a vacuum and "v" is the speed of light in the medium. Replacing the values:

`1.33=\frac{3*10^8\text{ m/s}}{v}`

Now we solve for "v":

`v=\frac{3*10^8\text{ m/s}}{1.33}`

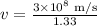
Solving the operation:

`v=2.26*10^8\text{ m/s}`

For part d. We will use the following formula:

`\lambda=(v)/(f)`

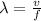
Where "v" is the speed and "f" is the frequency. Replacing we get:

`\lambda=\frac{2.26*10^8\text{ m/s}}{7.85*10^(16)s^(-1)}`

Solving the operations:

`\lambda=0.288*10^(-8)m`

For part e. The largest value of the angle of incidence that will result in refraction is 90 degrees.