Question

Sheldon is painting a wall in his house and is using a paint roller.The paint roller had a radius of 1 inch and a height of 8 inches.How many square inches of space Sheldon paint with one revolution of paint roller?Round to nearest tenths

Answer 1

The information we have about the paint roller:

Radius: r=1in

Height: h=8in

To find the answer to how many square inches of space he can paint with one revolution, it is useful to visualize the surface area of a cylinder:

The circles are the top and bottom of the cylinder, and the rectangle is the body of the cylinder (the paint roller). The area of this rectangle is the area that the paint roller will paint with one revolution.

Calculate the area of the rectangle:

To find the area, first, we need to find the length "L":

This length L is equal to the circumference of the circle defined as follows:

`L=2\pi r`

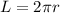
So to find L we substitute r=1in and pi=3.1416:

`\begin{gathered} L=2(3.14216)(1\text{ in)} \\ L=6.2832in \end{gathered}`

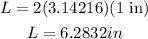
And finally, to find the area of the rectangle and thus, the area that the paint roller covers with one revolution, we multiply the length by the height:

`A=h* L`

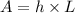
Where "A" is area.

Substituting h and L:

`\begin{gathered} A=8in*6.2832in \\ A=50.2656in^2 \end{gathered}`

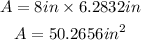
Rounding our answer to the nearest tenths:

`50.2656\approx50.3`

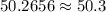
Answer: 50.3 square inches