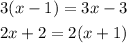Question

Which of the equations shown have infinitely many solutions ? Select all that apply. A. 3x-1=3x+1, B. 2x-1=1-2x, c 3x-2=2x-3, D 3(x-1)=3x-3, E. 2x+2=2(x+1), F. 3(x-2)=2(x-3)

Answer 1

The equations that have infinitely many solutions are;

`\begin{gathered} 3(x-1)=3x-3 \\ 2x+2=2(x+1) \end{gathered}`

Step-by-step explanation:

For an equation to have infinitely many solutions, the left-hand side of the equation and the right side of the equation must be equivalent/equal.

That means that the expression before the equal sign must be equivalent to the expression after the decimal.

such as;

`\begin{gathered} x=x \\ x+3=x+3 \\ 2x=2(x) \\ 4x+4=4(x+1) \end{gathered}`

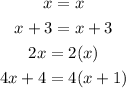
From the given equation, the equations that have their left and right sides equivalent are;

`\begin{gathered} 3(x-1)=3x-3 \\ 3x-3=3x-3 \\ \\ 2x+2=2(x+1) \\ 2x+2=2x+2 \end{gathered}`

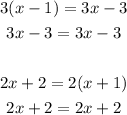
Therefore, the equations that have infinitely many solutions are;

`\begin{gathered} 3(x-1)=3x-3 \\ 2x+2=2(x+1) \end{gathered}`