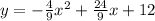
To find the maximun height (y) given a quadratic equation as above you find the coordinates of the vertex (maximum or minimun point of a parabola)
1. Use the next formula to find the x- coordinate of the vertex
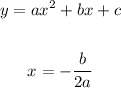
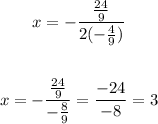
2. Use the value of x above to find y-coordinate in the vertex:
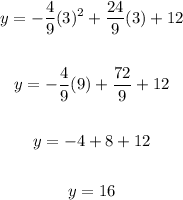
Then, the maximum height of the diver is 16 feet