Question

Is the following process correct? If not, which step is where the error occurs, justify your answer. Then rework the problem to find the correct answer.

Answer 1

We are given the following absolute value equation

`|4x-1|=5x+37`

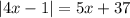
Let us solve the problem then we will compare it with the given solution.

`\begin{gathered} |4x-1|=5x+37 \\ 4x-1=\pm(5x+37) \end{gathered}`

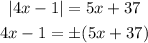
Now we will solve for the positive and negative sign separately

`\begin{gathered} 4x-1=5x+37 \\ 4x-5x=37+1 \\ -x=38 \\ x=-38 \end{gathered}`
`\begin{gathered} 4x-1=-5x-37 \\ 4x+5x=-37+1 \\ 9x=-36 \\ x=(-36)/(9) \\ x=-4 \end{gathered}`

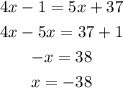
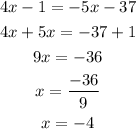
Comparing it with the given solution, there is an error on the left-hand side step 2. (the sign of 38 should be positive but in the figure, it is shown negative)

Now let us substitute the obtained x values into the original absolute value equation and check if they satisfy the equation.

For x = -4:

`\begin{gathered} |4(-4)-1|=5(-4)+37 \\ |-16-1|=-20+37 \\ |-17|=17 \\ 17=17 \end{gathered}`

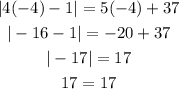
Hence, x = -4 is a valid solution.

For x = -38:

`\begin{gathered} |4(-38)-1|=5(-38)+37 \\ |-152-1|=-190+37 \\ |-153|=-153 \\ 153\\e-153 \end{gathered}`

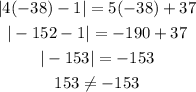
Hence, x = -38 is not a valid solution.

The above is an example of an extraneous solution.

An extraneous solution is a solution that we get during the process of solving an equation but it is not really the solution meaning that it does not satisfy the equation!

Therefore, x = -4 is the only solution to the given equation.