Answer:
y=5x
Explanation:
The slope-intercept form of the equation of a line is:
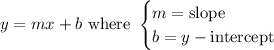
First, we find the slope of the line by picking two points from the line.
• The points are (0,0) and (3,15).
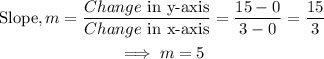
Next, the line crosses the y-axis at y=0.
Therefore, the y-intercept, b=0.
Substitute m=5 and b=0 into the slope-intercept form:
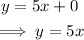
The equation that gives the proportional relationship of the graph is y=5x.