SOLUTION
Consider the image below,
The lenght of the compass is the radius, using a lenght of 5 unit, we have circle below as the sphere .
Where
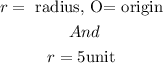
Using the formula, we have
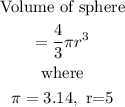
Substitute into the formula, we have

Therefore
The volume of the sphere is 523.33 cubic unit