6.
(a)
The slope for the side AB is:

The slope for the side BC is:
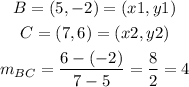
The slope for the side DC is:
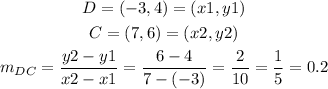
And the slope for AD is:
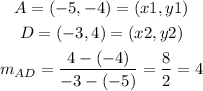
(b) According to the previous results:
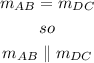

(c) Since it has two pairs of parallel sides, also, The opposite sides are of equal length, we can conclude that this figure is a parallelogram