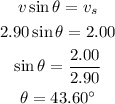Question

Sheena can row a boat at 2.90 mi/h in still water. She needs to cross a river that is 1.20 mi wide with a current flowing at 2.00 mi/h. Not having her calculator ready, she guesses that to go straight across, she should head upstream at an angle of 25.0° from the direction straight across the river.What is her speed with respect to the starting point on the bank?How long does it take her to cross the river?How far upstream or downstream from her starting point will she reach the opposite bank? If upstream, enter a positive value and if downstream, enter a negative value.In order to go straight across, what angle upstream should she have headed?

Answer 1

Given

v = 2.90 mi/h

x = 1.20 mi

vs = 2.0 mi/h

θ = 25°

Procedure

Part a)

Velocity of the boat with respect to water stream is given as

`\begin{gathered} v_b=v-v_s \\ v_b=(2.90\cdot\sin 25-2.00)\hat{j}+2.90\cdot\cos 25\hat{i} \\ v_b=-0.77\hat{j}+2.62\hat{i} \end{gathered}`

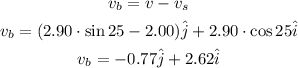
magnitude of the speed is given as

`\begin{gathered} v_b=\sqrt[]{0.77^2+2.62^2} \\ v_b=2.73mi/h \end{gathered}`

Part b)

Time to cross the river is given as:

`\begin{gathered} t=(x)/(v_x) \\ t=(1.2mi)/(2.90\cdot\cos25) \\ t=0.46h \end{gathered}`

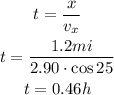
Part c)

Distance moved by boat in downstream is given as

`\begin{gathered} x=v_yt \\ x=-0.77\cdot0.46 \\ x=-0.354mi \end{gathered}`

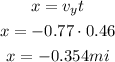
Part d)

In order to go straight, we must net speed along the stream must be zero

so we will have

`\begin{gathered} v\sin \theta=v_s \\ 2.90\sin \theta=2.00_{} \\ \sin \theta=(2.00)/(2.90) \\ \theta=43.60^(\circ) \end{gathered}`