Let the amount of 30% acid solution be a
Let the amount of 60% acid solution be b
Given, "a" and "b" mixed together gives 570 liters of 31% acid. We can write:

Also, we know 30% acid and 60% acid amounts to 570 liters, thus:
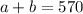
The first equation becomes:
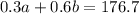
We can solve the second equation for a:

Putting this into the first equation, we can solve for b. The steps are shown below:

So, a will be:
a = 570 - b
a = 570 - 19
a = 551
Thus,
551 Liters of 30% acid solution and 19 Liters of 60% acid solution need to be mixed.