Question

I need some explanation on how to do piece wise functions? Where do I even start with this equation, can you explain this step by step? Including breaking down the graphing of absolute functions?

Answer 1

A piecewise function is basically a function that behaves differently at different domain intervals.

The given piecewise function is

`\begin{cases}2x\quad \quad \quad \quad \quad \quad x\le3 \\ (1)/(3)x^2-2x+9\quad x>3\end{cases}`

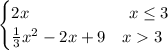
As you can see, the function has a different expression for the interval x is less than or equal to 3 and a different expression for the interval x is greater than 3.

The easiest way to determine which graph corresponds to the given piecewise function is to evaluate the piecewise function at different values of x and graph it.

Evaluate the piecewise function for the interval x is less than or equal to 3.

`\begin{gathered} 2x \\ x=1\rightarrow2(1)=2 \\ x=2\rightarrow2(2)=4 \\ x=3\rightarrow2(3)=6 \end{gathered}`

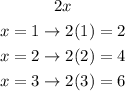
Evaluate the piecewise function for the interval x is greater than 3.

`\begin{gathered} (1)/(3)x^2-2x+9 \\ x=4\rightarrow(1)/(3)(4)^2-2(4)+9=6.33 \\ x=6\rightarrow(1)/(3)(6)^2-2(6)+9=9 \\ x=8\rightarrow(1)/(3)(8)^2-2(8)+9=14.33 \end{gathered}`

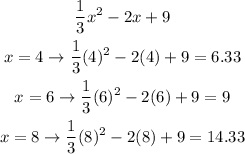
Now, let us graph these points

As you can see from the graph, it matches with the graph of the 2nd option.

Therefore, the correct graph of the given piecewise function is the 2nd graph.