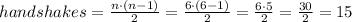Question

At a party 15 handshakes took place. Each person shook hands exactly once with each of the other present. How many people were at the party?

Answer 1

2 people => 1 handshake (AB)

3 people => 3 handshakes (AB, BC, AC)

4 people => 6 handshakes (AB, AC, AD, BC, BD, CD)

Do you see a pattern here?

We can write a general formula for this

`handshakes=(n\cdot(n-1))/(2)`

Since we are given that there were 15 handshakes

`15=(n\cdot(n-1))/(2)`
`\begin{gathered} 2\cdot15=n\cdot(n-1) \\ 30=n\cdot(n-1) \\ 30=6\cdot(6-1) \\ 30=6\cdot(5) \\ 30=30 \end{gathered}`

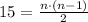
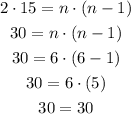
This means that n = 6 people were present at the party.

You can substitute n = 6 into the above formula and you will notice that it will give 15 handshakes

`handshakes=(n\cdot(n-1))/(2)=(6\cdot(6-1))/(2)=(6\cdot5)/(2)=(30)/(2)=15`