As given by the question
There are given that the function:

Now,
To find the critical point, differentiate the given function with respect to x and put the result of function equal to zero
So,
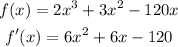
Then,
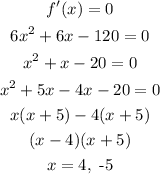
Now,
To find the y-coordinate, we need to substitute the above value, x = 4, -5, into the function f(x)
So,
First put x = 4 into the given function:
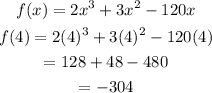
And,
Put x = -5 into the function f(x):
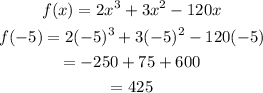
Hence, the critical point is, (4, -304) and (-5, 425).
Now,
To find the local maxima and local minima, we need to find the second derivative of the given function:;
So,

Now,
The put the value from critical point into the above function to check whether it is maxima or minima.
So,
First put x = 4 into above function:
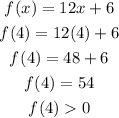
And,
Put x = -5 into the above function
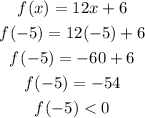
Then,
According to the concept, if f''(x)>0 then it is local minima function and if f''(x)<0, then it is local maxima function
Hence, the given function is local maxima at (-5, 425) and the value is -54 and the given function is local minima at point (4, -304) and the value is 54.