Question

A 77 kg student traveling in a car with a constant velocity has a kinetic energy of 1.7 104 J. What is the speedometer reading of the car in km/h? answer with:_____km/h

Answer 1

75.65 km/h

Step-by-step explanation

Given:

• The student's mass, m = 77 kg

,

• The kinetic energy of the student in the car, KE = 1.7 x 10⁴ J

Find:

• The speed read in the speedometer of the car, which is the speed of the student, v (in km/h)

The kinetic energy of an object with mass m, traveling at a speed v, is,

`KE=(1)/(2)mv^2`

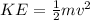
Solving for v,

`v=\sqrt{(2KE)/(m)}`

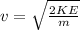
Replace the known values and solve,

`v=\sqrt{(2\cdot1.7\cdot10^4J)/(77kg)}\approx21.013m/s`

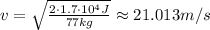
Note that because the kinetic energy is given in Joules - which is equivalent to kg*m²/s², the speed we found is in m/s. Now, knowing that there are 3600 seconds in 1 hour and that 1 km is equivalent to 1000 m, we can convert this to km/s,

`v=21.013(m)/(s)\cdot(3600s)/(1h)\cdot(1km)/(1000m)\approx75.65km/h`

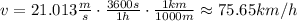
Hence, the speedometer reading of the car is 75.65 km/h, rounded to the nearest hundredth.