Answer:
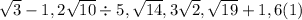
Explanation:
Given the irrational numbers:
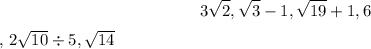
In order to arrange the numbers from the least to the greatest, we convert each number into its decimal equivalent.
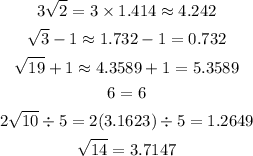
Finally, sort these numbers in ascending order..
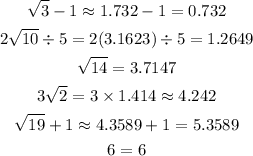
The given numbers in ascending order is:
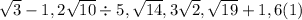
Note: In your solution, you can make the conversion of each irrational begin on a new line.