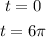Question

On a particular day, the amount of untreated water coming into the plant can be modeled by f(t) = 100 + 30cos(t/6) where t is in hours since midnight and f(t) represents thousands of gallons of water. The amount of treated water at any given time, t, can be modeled by g(t) = 30e^cos(t/2)a) Define a new function, a′(t), that would represent the amount of untreated water inside the plant, at any given time, t.b) Find a′ (t).c) Determine the critical values of this function over the interval [0, 24).

Answer 1

a)The amount of untreated water inside the plant will be the difference between the difference f(t) - g(t), then, a(t) can be defined as follows:

`a(t)=100+30cos((t)/(6))-30e^{cos((t)/(2))}`

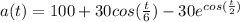
b) the derivative of a(t) is the following:

`a^(\prime)(t)=-5sin((t)/(6))+15sin((t)/(2))e^{cos((t)/(2))}`

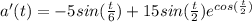
c) the critical values of a(t) over the interval [0, 24) are:

`\begin{gathered} t=0 \\ t=6\pi \end{gathered}`