Question

A ball is thrown from an initial height of 6 feet with an initial upward velocity of 21 ft/s. The ball's heighth (in feet) after t seconds is given by the following,6+21 167Find all values of t for which the ball's height is 12 feet.Round your answer(s) to the hearest hundredth(If there is more than one answer, use the "or" button.)

Answer 1

The given expression in the question is

`h=6+21t-16t^2`

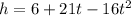
with the value of h given as

`h=12ft`

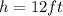
By equating both equations, we will have

`\begin{gathered} 12=6+21t-16t^2 \\ 12-6-21t+16t^2=0 \\ 6-21t+16t^2=0 \\ 16t^2-21t+6=0 \end{gathered}`

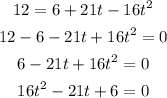
To find the value of t we will use the quadratic formula of

`ax^2+bx+c=0`

which is

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where} \\ a=16 \\ b=-21 \\ c=6 \end{gathered}`

By substitution, we will have

`\begin{gathered} t=\frac{-(-21)\pm\sqrt[]{(-21)^2-4*16*6}}{2*16} \\ t=\frac{21\pm\sqrt[]{441-384}}{32} \\ t=\frac{21\pm\sqrt[]{57}}{32} \\ t=(21\pm7.5498)/(32) \\ t=(21+7.5498)/(32)\text{ or t=}(21-7.5498)/(32) \\ t=\frac{28.5498}{32\text{ }}\text{ or }t=\frac{13.4502}{32\text{ }} \\ t=0.89\text{ or t=0.42} \end{gathered}`

Alternatively, Solving the equation graphically we will have

Therefore,

The values of t( to the nearest hundredth) t= 0.89sec or 0.42sec