Question

ALTAThe graph shown compares the rent Andrew and Dave pay for renting bikes from different stores,Andrew's and Dave'sBike Rentalsу13DaveAndrew11Rent Paid (dollars)2319117HoursAfter how many hours would the amount Andrew and Dave pay for the rentals be equal?

Answer 1

We have the following:

The first thing is to calculate the equation by means of the graph.

For Andrew, we can see that he starts at $ 3 and every hour that passes, he charges $ 2, therefore the equation is:

`y=3+2x`

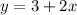
where x is the number of hours.

For Dave, we can see that he starts at $ 6 and every hour that passes, he charges $ 1.5, therefore the equation is:

`y=6+1.5x`

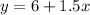
where x is the number of hours.

to calculate the number of hours when the value is equal, we must match the equations like this

`\begin{gathered} 3+2x=6+1.5x \\ 2x-1.5x=6-3 \\ 0.5x=3 \\ x=(3)/(0.5)=6 \end{gathered}`

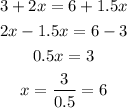
Which means that at 6 hours they have the same price