Question

36. The widths of platinum samples manufactured at a factory are normally distributed, with a mean of 1.3 cm and a standard deviation of 0.3 cm. Find the z-scores that correspond to each of the following widths. Round your answers to the nearest hundredth, if necessary.(a) 1.7 cmz = (b) 0.9 cmz =

Answer 1

(a) For a width of 1.7 cm, the z-score is approximately 1.33.

(b) For a width of 0.9 cm, the z-score is approximately -1.33.

To find the z-scores for each width, we'll use the formula for calculating z-scores:

`\[ z = \frac{{\text{Value} - \text{Mean}}}{{\text{Standard Deviation}}} \]`

Given:

Mean
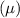`(\(\mu\))` = 1.3 cm

Standard Deviation
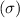`(\(\sigma\))` = 0.3 cm

(a) Width of 1.7 cm

`\[ z = \frac{{\text{Value} - \text{Mean}}}{{\text{Standard Deviation}}} \]`

`\[ z = \frac{{1.7 - 1.3}}{{0.3}} \]`

`\[ z = \frac{{0.4}}{{0.3}} \]`

`\[ z \approx 1.33 \]`

Therefore, the z-score for a width of 1.7 cm is approximately 1.33.

(b) Width of 0.9 cm

`\[ z = \frac{{\text{Value} - \text{Mean}}}{{\text{Standard Deviation}}} \]`

`\[ z = \frac{{0.9 - 1.3}}{{0.3}} \]`

`\[ z = \frac{{-0.4}}{{0.3}} \]`

`\[ z \approx -1.33 \]`

Therefore, the z-score for a width of 0.9 cm is approximately -1.33.

Answer 2

Part (a)

Using the formula for the z-scores and the information given, we have:

`\begin{gathered} \text{ z-score=}\frac{\text{ data value }-\text{ mean}}{\text{ standard deviation }} \\ \text{ z-score=}\frac{1.7\text{ cm }-\text{ 1.3 cm}}{0.3\text{ cm}} \\ \text{ z-score=}\frac{0.4\text{ cm}}{0.3\text{ cm}}\text{ (Subtracting)} \\ \text{ z-score=1.33 (Dividing)} \\ \text{The z-score for 1.7 cm is 1.33 rounding to the nearest hundredth.} \end{gathered}`

Part (b)

Using the formula for the z-scores and the information given, we have:

`\begin{gathered} \text{ z-score=}\frac{\text{ data value }-\text{ mean}}{\text{ standard deviation }} \\ \text{z-score=}\frac{\text{ 0.9 cm }-1.3\text{ cm}}{\text{ 0.3 }}\text{ (Replacing the values)} \\ \text{z-score=}\frac{\text{ }-0.4}{\text{ 0.3 }}\text{ (Subtracting)} \\ \text{ z-score= }-1.33 \\ \text{The z-score for 0.9 cm is -1.33 rounding to the nearest hundredth.} \end{gathered}`