This is a compound interest question and we have been given:
Principal (P) = $24000
Rate (r) = 7.25%
Years (t) = 10
However, we are told this value is compounded continuously. This means that for every infinitesimal time period, the value keeps being compounded.
The formula for finding the compound interest is:
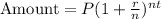
But because the compounding period is continuous and therefore, infinitesimal,
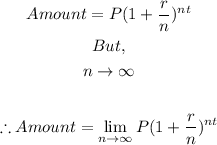
This is similar to the general formula for Euler's number (e) which is:
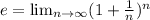
Thus, we can re-write the Amount formula in terms of e:

Therefore, we can find the amount of money in the account after 10 years:
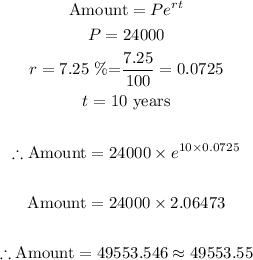
Therefore the amount after compounding continuously for 10 years is:
$49553.55