We know that the painting increase its value by 5% each year.
So, if P(1) is the value the next year and P(0) is the actual value ($27,400) we can write:
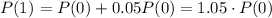
In the same way, the following year, it will increase another 5% over its value:
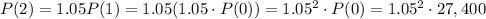
We can generalize this as:
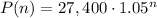
For n=3 (3 years) we will have a value of:
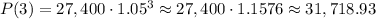
Answer: the value of the painting in 3 years is expected to be $31,718.93.