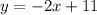Question

write the equation of the line passing through the given points write your awnser in slope intercept form Y=mx+b (5 1) and (-3 17)

Answer 1

The given points are (5, 1) and (-3, 17).

First, we have to find the slope using the following formula.

`m=(y_2-y_1)/(x_2-x_1)`

Where,

`\begin{gathered} x_1=5 \\ x_2=-3 \\ y_1=1 \\ y_2=17 \end{gathered}`

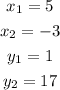
Let's use the coordinates above to find the slope.

`m=(17-1)/(-3-5)=(16)/(-8)\Rightarrow m=-2`

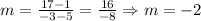
The slope is -2.

Now, we use the point-slope formula to find the equation.

`y-y_1=m(x-x_1)`

Let's use the same coordinates x_1 and y_1, and the slope m = -2.

`y-1=-2(x-5)`

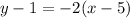
Now, we solve for y to express the equation in slope-intercept form.

`y-1=-2x+10\Rightarrow y=-2x+10+1\Rightarrow y=-2x+11`

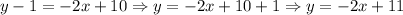
Therefore, the slope-intercept form of the equation is

`y=-2x+11`